Diffie-Hellman 算法分析及其改进

发表于 更新于 分类于 ， 本文字数： 731 阅读时长 ≈ 1 分钟

概述

Diffie-Hellman 算法（简称 DH 算法）是最早的密钥交换算法，用于通信双方在非安全的信道中安全地交换密钥，用于加密后续的通信消息。该算法及其衍生算法在安全领域中应用很多，包括 TLS、IPSec、IKE 及 Bluetooth 网络和通信协议等。

匿名 DH 算法

使用基本的 Diffie-Hellman 算法（见上节），在向对方发送 Diffie-Hellman 公钥参数时不进行认证。因此该方法容易遭受中间人攻击。

瞬时 DH 算法

用于创建临时密钥，在这种方法中，Diffie-Hellman 公钥在交换时使用发送者的 RSA 或 DSS 或 ECC 私钥签名。接收者使用相应的公钥验证签名。

基于 RSA 的密钥交换算法

RSA 密钥交换算法使用文字描述如下：
a. 客户端向服务器端发起“交换请求（或证书请求）”，服务器首先回复公钥到客户端。
b. 客户端使用随机数生成密钥 S，使用收到的公钥进行加密，生成 C，把 C 发送到服务器。
c. 服务器收到 C，使用公钥对应的私钥进行解密，得到 S。
d. 客户端和服务器端得到了共享密钥 S （预主密钥）

图示如下：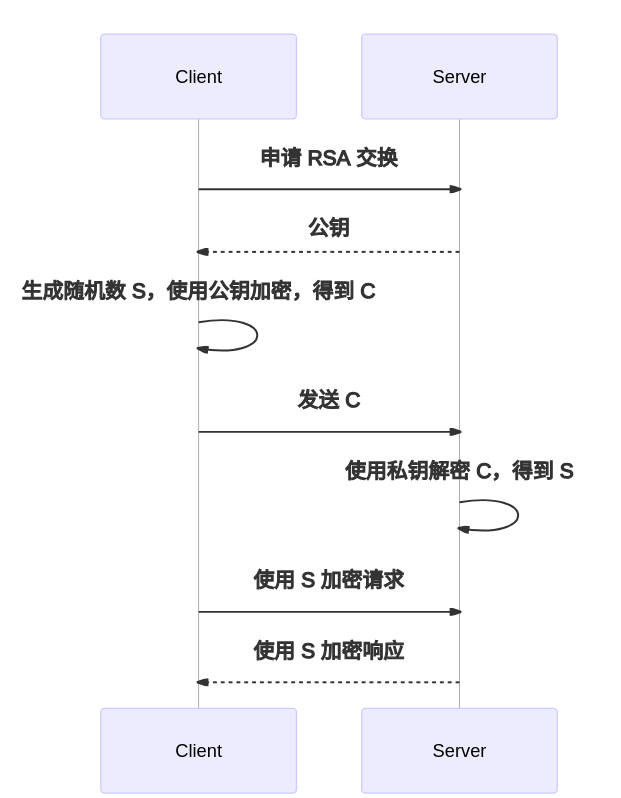

SSL 协议中，服务器发送的公钥在 SSL 中是通过certificate报文发送的，certificate中的包含了公钥。C 是通过Client key exchange报文发送的。

Oakley 算法

Oakley 算法是 IETF 对 DH 算法的改进，其特性包括：

  • 采用称为 cookie 程序的机制以对抗阻塞攻击。
  • 允许双方协商一个全局参数集合。
  • 利用现时确保抵抗重放攻击。
  • 能够交换 Diffie-Hellman 公开密钥。
  • 对 Diffie-Hellman 交换进行鉴别以防止中间人攻击。